Finite Difference Solution to the Acoustic Wave Equation
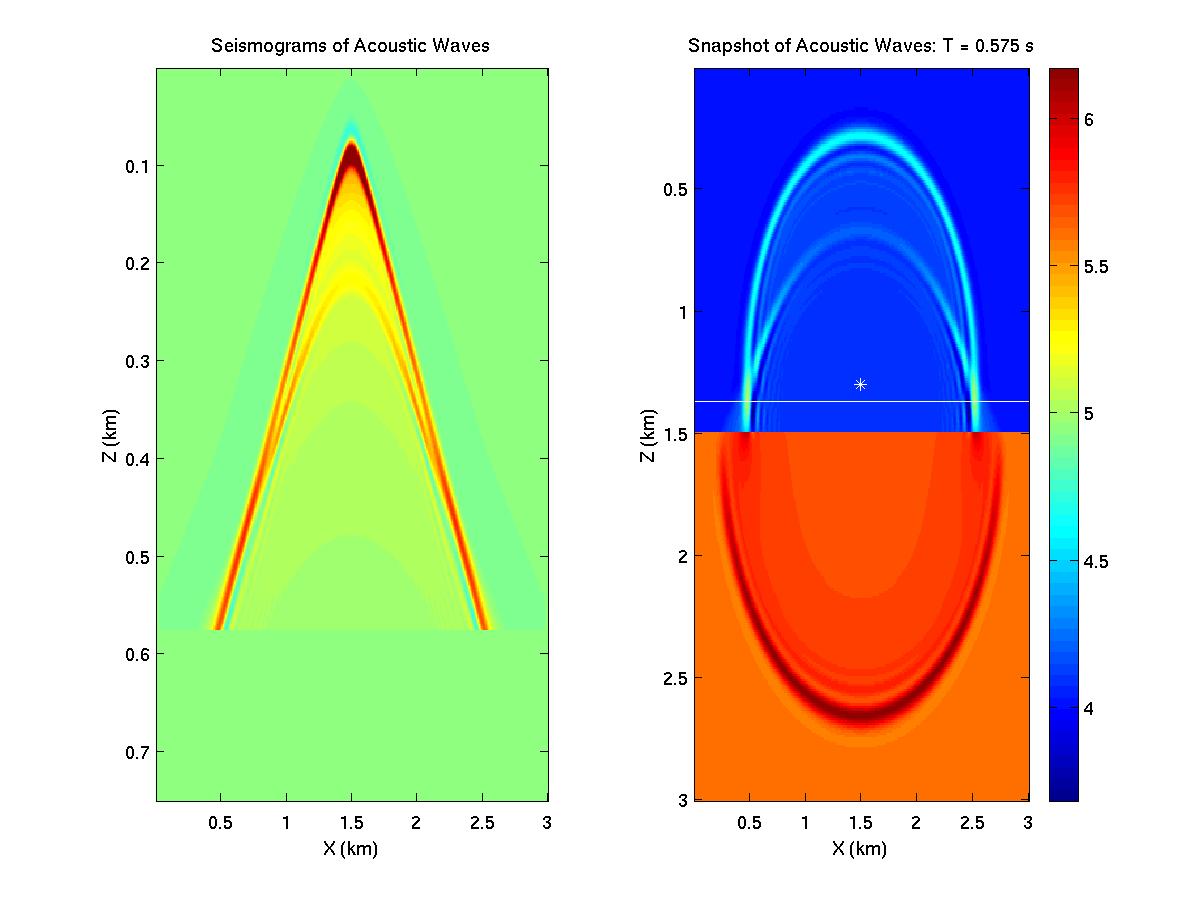
Figure 1. Seismograms and snapshot associated with a line source placed
just above the 2-layer medium.
Objective: Calculate synthetic seismograms by a 2-2 FD solution to the wave equation. Learn how space and time sampling increments affect the output.
Skill Learned: Implementation, design and construction of synthetic seismograms by finite-difference solutions to the wave equation.
Procedure:
- Download the codes fd.m and plt.m and type "fd". This will generate the synthetic seismograms and snapshots for a 2-layer medium.
Exercises:
- From the snapshots estimate the wavelengths of the waves in the top and bottom layers (Use the zoom facility in MATLAB). Compare these wavelengths to the theoretical estimates from lambda=c/f..
- Change ABCs so they are on all sides except for the top boundary..make the top a free surface. Repeat simulations. Describe the changes in snapshots compared to previous simulation.
- Identify the direct, refraction, and reflection waves in the snapshots and the seismograms. Estimate their apparent velocities. Explain why the reflection waves moveout with the slowest apparent velocities.
- Raise the frequency of the source by 50% and repeat the simulations. Comment on loss of accuracy and give rationale.
- Choose a dt value that violates stability. Rerun simulations. What happens?
- The head wave arrival is extremely weak, as predicted by theory. However, a diving wave that gets trapped in a thin interface just below the refracting interface can boost up the amplitude. Adjust the velocity model so there is a thin layer (10 points thick) just below the original interface. make sure the velocity is the average between layer 1 and 2. Now rerun the fd.m code. Is there a difference in head wave amplitudes? Change models until you get a satisfactory amplitude.
- Lab reports should be written in a style similar to a scientific paper so that the reader can clearly understand what you did and be convinced that your procedure is correct. All answers to questions should be written in complete sentences. The reader should be given enough detail so that they can reproduce your results if they had your code. Each question or sub-exercise should be stated, the answers should be written in complete sentences, figures should have labels on all axis with correct units, a title label should accompany each graph, and each figure should be labeled with a number and a caption. Show any work that you might use if a mathematical derivation is called for.