Spectral Deconvolution Lab
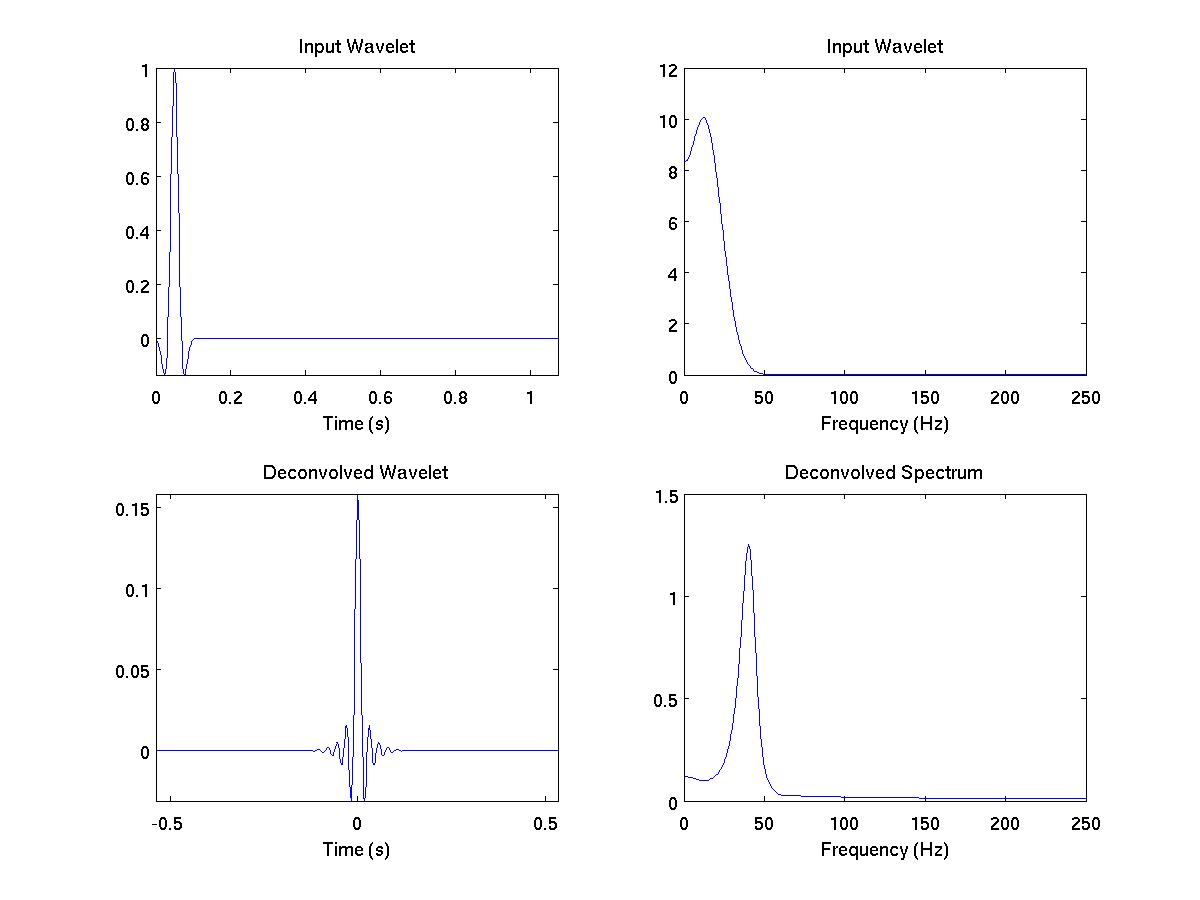
Figure 1.
The a) input time series and b) output after application of spectral deconvolution.
Theory: Given an input signal x, find the deconvolution
filter f by spectral division f=x*/(|x|2+ eps),
where eps is a small positive number known as the damping parameter (see Yilmaz, 2001).
Objective: Practice the craft of spectral deconvolution
of a signal.
Procedure:
- Execute the command deconsimp.m.
- Change values of damping parameter eps1. Explain what happens
to deconvolved wavelet if
eps1 is to small. Explain what happens if eps is too large.
Note, as eps becomes really large the inverse
filter f is a constant for a zero-phase x and is an all pass filter.
Thus, larger values of eps lead to deconvolved results with fatter main lobes
and smaller side lobes. As eps becomes smaller the main lobe thins and the side lobes become more pronounced.
- Add noise to wavelet by the command
x1=3*x./max(x)+rand(1,nt)-.5; plot(x1);
and repeat exercise. What is the effect of random noise?
- Download the shot gather CSG and type "load CSG".
To display the shot gather type "CSG=CSG/max(CSG(:)); clim=[-.03 .03];imagesc(CSG',clim);".
Extract one of the traces
and autocorrelate it, then truncate the autocorrelation after the 2nd zero crossing.
This truncated wavelet will now be your estimated input wavelet.
Find the inverse filter f to this correlation wavelet
and use it to deconvolve the autocorrelation trace.
Compare the deconvolved autocorrelation trace to original autocorrelation trace.
- A more robust estimate of the decon filter might be obtained by averaging
truncated autocorrelation signals for a number of different traces. Use
averaging to construct your new inverse filter and deconvolve the autocorrelated
traces. Compare the new results to the results from the previous question.
- A trick that is almost always used
after any deconvolution process is to bandpass filter the deconvolved results, where the passband is
over the frequency range of the estimated signal.
